I have, potentially,
my first game on Monday. It's at a local
gaming store, but since it's during the weekday, it should be relatively
quiet. Because of this, I have been
frantically working at the trade tables to get them into a useable state - it
also keeps me distracted from the schoolwork that needs to be done this weekend
as well.
I was completing the
second step in the process, aggregating all of my world's references into
thematic groups with some rudimentary determination of goods that require no
processing, when I ran into two problems.
Before I get into
this, if you are not familiar with Alexis' trade tables, I suggest you fix that
- the following discussion will make no sense if you don't.
The first problem
was with the valuation of gold. This is
the first calculation on the sheet, and it's important because it determines
the price, in copper pieces, of 1 reference's worth of goods. For the sake of simplicity, I am calling that
quantity a crop. Right now, a resource's crop size is
determined by dividing the global production of that resource by all of the
references for it (on a global scale).
It struck me as a
little odd that the gold crop had no direct bearing on the local value of
gold. Then I started digging a little
further and it appeared that the price of gold would only fluctuate based upon
.002*local/global, where local is the number of local references of gold and
global is the total number of gold references.
This seemed strange to me, but I continued forward.
What convinced me
that this was a problem, though, was the double-conversion to coinage seen
whenever the price of a good was to be generated. The formula for an arbitrary good looked
something like this,
Where refVal is the
value in copper pieces of 1 reference, calculated as above and production is
the global quantity of a good produced.
This simplifies to
Which means that the
local amount of a reference has no significant bearing upon its price. Additionally, since refVal has already
converted from oz. gold to copper coins, the additional coin conversion at the
end of the equation is extraneous.
Which means that I
needed a new way to value gold and a new way to assign a coin value to 1 unit
of a resource. I called in my roommate
and we spent half the night yesterday/this morning fighting through this to find
a solution. And find one we did.
The challenge of
this problem is that there are so few actual variables that depend upon
location - every meaningful combination of them resulted in their cancellation,
which defeated the purpose of the proposed improvement. We eventually hit upon the idea of
incorporating a new variable: the power of the market in question, determined
by the sum of all the local references (i.e. all the references in the world
altered by their distance from the market in question). With this in hand, we returned to the
problem.
For gold, we have
I'll walk you
through this equation. The
product/global term gives us the crop size - how many units of a good are worth
1 reference. We then multiply our crop
size by the power of our market which tells us how many oz. of gold our economy
is worth (since 1 reference is equal in value to any other reference, we have
product/global*power value in our system as a whole). We divide this number by how many references
of gold we actually possess, local, and this gives us a ratio of the total
value of our system in gold by how many references for gold we actually
have. We convert this to copper coins
and are done.
Now to tackle
valuing goods. Working this morning, I
constructed the following expression:
The first term
calculates the value of the goods on hand in copper pieces. The second term scales that price by how
powerful our market is and how abundant the resource is - a resource with fewer
references will have a higher price than one with many, and a more powerful
market (drawing more things from more places) will command lower prices
overall.
Alexis' explanations
of his own steps are as good, if not better than mine. But the units of all of these expressions
work out, and now each good's price is influenced by the market's power and the
global and local reference values, increasing site-specific prices.
Of course, due to
the probabilistic process through which I generated my references, I may have
some correcting to do (I needed to add a bunch of iron references, for
example), and that may necessitate either adding more references or modifying
the production totals in order for the economy to work in the way that I need,
but I am much happier with these expressions.
Also, as a side note, VLOOKUP is a godsend in this work. No more hunting for appropriate references!



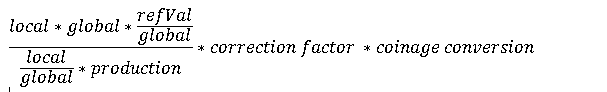



I wouldn't really call "power" a new variable: Alexis' 2010 work on his Trade system has a different value & calculation for the factor which became ".02 adjustment for rarity;" that is, "we will need an adjustment for the relative rarity of gold in the market as compared to other markets. This is the adjustment for rarity: the total number of references divided by local references, multiplied by 0.02, plus 1..." When I was first reading the 2010 Trade Table work, the factor was more like .05, but it was applied differently.
ReplyDeleteIt was a little "strange" to me, as well, to have this factor and not to have the reasoning behind it. So I changed it, drastically, for my own purposes.
"(Global) Valuation" for me is 100% of all the market. The "(Local) Market Valuation" then is 100% of this ceiling, MINUS r/R, where 'r'=local references and 'R'=total references. That is, I determined that the DISCOUNT from the theoretical Global Market Ceiling is the percentage of that Market's references to the Global references.
It works VERY well: a market with ~30% of the Gold output gives me just under 11 silver pieces to the gold piece; a market with only 8% gives just under 15 silver pieces to the gold piece.
This calculation gives a "Currency" market which shows me at a glance what the relative purchasing power is across each location; everything else falls into place, without a vague ".02" popping out.
(I'm trying to leave work and type this at the same time; we'll talk more, I'm sure.)
Thanks for the comment - I didn't think this was a new idea, and it makes sense that I'm rehashing terrain Alexis has already crossed.
ReplyDeleteWould you mind posting your version of the pricing expression so that I can compare? I'm not quite following your formulation.
It sounds to me like you are allowing variations in the price of silver determine the coinage exchange? I'm curious what you feel the benefit is from that as opposed to absorbing the price difference entirely within the cost of the good (without the currency exchange rates mediating the price difference).
Not exactly; I sort of make Gold bullion one good, then Gold coin another. The number above is the ratio in a silver standard, by bullion-weights; coinage variation stays standard per-empire. After gold has been given a value in Coinage (via silver wt => silver piece), I still do all the local market-size-strength manipulation per good, as well. The benefit is that I get travelers from gold-rich lands carry (and spend!) more coins, and gold-poor locations will appear relatively coin-light.
ReplyDeleteDon't mind sharing at all; here's a less-messy Google Sheet.
(Didn't mean to make you feel badly about "new", of course. There's nothing new under the sun!)
Interesting. Thank you for being so kind to share. That's not something with which I want to tinker right now, but it is nice to know that option is available to me.
ReplyDeleteAnd being original is greatly overrated. I am quite happy to blatantly copy Alexis' work. :-)